Generating Realistic Heights Distributions for Terrain Generation in C# for Unity
Published
When generating terrain, it is common to use Perlin Noise, but most of the time it’s not possible to use it as is: the tiling and the patterns it exhibits are obvious so we need to process it.
The alternative is to use a different approach: sample from a real height distribution.
This is the approach used in Designer Worlds: Procedural Generation of Infinite Terrain from Real-World Elevation Data, and it uses the following steps:
- Get real world elevation data
- Normalize the elevation data to a specified range
- Create bins
- Sample from the bins using the value given by Perlin Noise, or any other layered noise approach.
We’ll use this approach to generate our terrain, with a small twist: we’ll be generating fake elevation maps by stacking different probability functions. This allows us to avoid depending on real data, which requires to be downloaded and preprocessed, and could potentially get more details (while I’m using bins of data here, the probability density functions are continuous so you could avoid aliasing). This makes collaboration, sharing and applying modifications much easier (for example Normal and Gamma distributions have only 2 parameters, while the Uniform Distribution has none).
The intent is to produce distributions that mimic real world data, while using a layered noise function will allow for local consistency. Real world elevation data distributions can be extremely varied as we can see below.
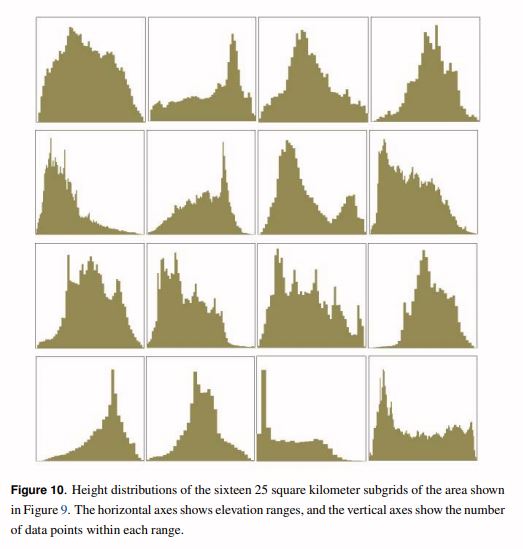
As you can see from the samples, real elevation data very vaguely ressembles a normal distribution: while there is usually a “central” or “main” peak in the data, we can see that some of these elevations data seem to follow a multimodal distribution, while others have fat tails, or show a lot of skewness.
From this quick overview, this explains why we want to use gamma and uniform distributions:
- A Gamma distribution allows us to set a skewness and a kurtosis (the ‘tailedness’ of the distribution), which is not something that can immediately be done with a normal distribution
- The Uniform distribution will help us to add noise, and also to thicken the base of the cumulative distribution
By setting several distributions together, and weighting their participation in the total draws, we’ll end up with a simple but extremely powerful tool to generate fake elevation data that mimics real-world data.
I made a quick implementation by creating a Scriptable Object to define Distributions data, which exposes the type of the distribution (uniform, normal or gamma), and its parameters (range for the uniform distribution, mean and variance for normal, and scale/skew for gamma). I added the Accord Framework to my build to have access to different probability distributions.
using System.Collections.Generic;
using UnityEngine;
using Accord.Statistics.Distributions;
using Accord.Statistics.Distributions.Univariate;
public enum DistributionTypes
{
Uniform,
Normal,
Gamma
}
[CreateAssetMenu(fileName = "DistributionData", menuName = "Distributions/new Distribution Data")]
public class DistributionData : ScriptableObject
{
public DistributionTypes mDistributionType;
public int mNbDraws;
public List<float> mParameters;
public List<float> Draw()
{
return Draw(mNbDraws);
}
public List<float> Draw(int nbDraws)
{
List<float> draws;
switch (mDistributionType)
{
case DistributionTypes.Uniform:
draws = _DrawUniform(nbDraws);
break;
case DistributionTypes.Normal:
draws = _DrawNormal(nbDraws);
break;
case DistributionTypes.Gamma:
draws = _DrawGamma(nbDraws);
break;
default:
Debug.LogError("Invalid Distribution Type. Defaulting to Uniform");
draws = _DrawUniform(nbDraws);
break;
}
return draws;
}
private List<float> _Draw(ISampleableDistribution<double> distribution, int nbDraws)
{
List<float> draws = new List<float>();
for (int i = 0; i < nbDraws; i++)
{
draws.Add((float)distribution.Generate());
}
return draws;
}
private List<float> _DrawUniform(int nbDraws)
{
UniformContinuousDistribution distrib = new UniformContinuousDistribution(mParameters[0], mParameters[1]);
return _Draw(distrib, nbDraws);
}
private List<float> _DrawNormal(int nbDraws)
{
NormalDistribution distrib = new NormalDistribution(mParameters[0], mParameters[1]);
return _Draw(distrib, nbDraws);
}
private List<float> _DrawGamma(int nbDraws)
{
GammaDistribution distrib = new GammaDistribution(mParameters[0], mParameters[1]);
return _Draw(distrib, nbDraws);
}
}
Then you’ll need to write a class that will take as input a list of DistributionData Scriptable Objects defining distributions, perform draws on all of them, rescale the data between 0 and 1 and bin the data, according to a chosen number of bins.
Once you have this binned data, you can compute cumulative probabilities, and perform draws.
To draw from our generated distribution, we’ll use perlin noise or some kind of layered noise to ensure a level of local consistency.
This model gives us a lot of flexibility, and we can have some interesting results with some tweaking.

Improvements
The code above describes a simple implementation, and using Scriptable Objects feels extremely awkward when trying out parameters, I’d like to implement a custom editor in my generator to handle parameter changes in a convenient manner.
For my version, I only used Normal, Gamma and Uniform distributions, but there are many more you can use, see for yourself!
We’re really not concerned about “statistics” and “probabilities”, we are only focusing on the shape of the distributions in order to easily emulate complex real world distributions.
I believe this can also be used as a base for a terrain generating that is easy to use for designers, and I hope to release such a tool in the future, along with different generated samples. Stay tuned!