Implementing the ELO Ranking System in C# for Unity

Published Oct 17, 2020

Ranking systems follow a basic principle: if your ranking is higher than your opponent’s, then that means you are more likely to win against him in a match; your ranking is therefore a measure of your skill level.

For convenience, many ranking system do not use an ordinal system (aka 1st, 2nd…) but rely on a sum of points: the true skill level of a player cannot be perfectly deduced, but it can be approximated by adding and substracting points from the player’s total. These variations in total points are also weighted by the computed probability of winning and should stabilize around a number that accurately represents the player’s skill.

This kind of system is called “self-correcting” and we’ll now see how to implement it.

UPDATE:
The C# code is now available on github.

There’s also a version in python.
The python version includes code to simulate rounds, the result can be viewed in the gif below.

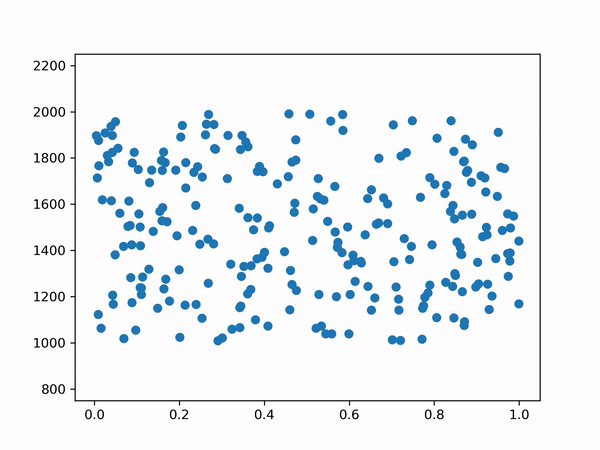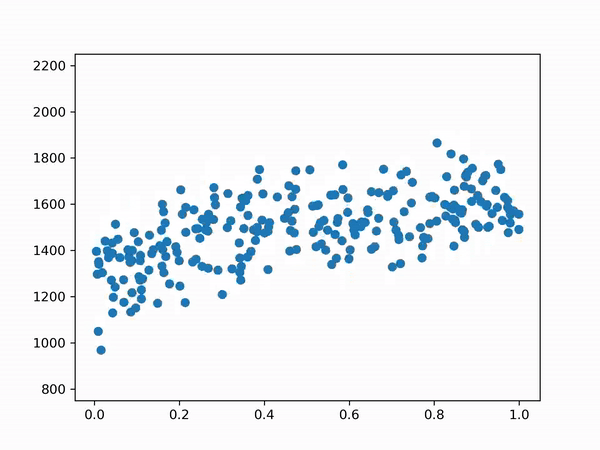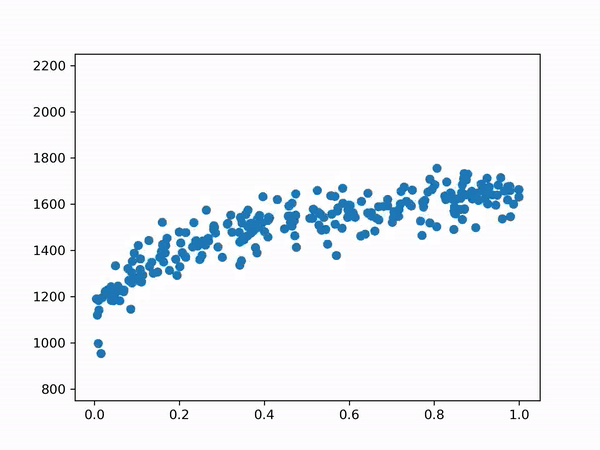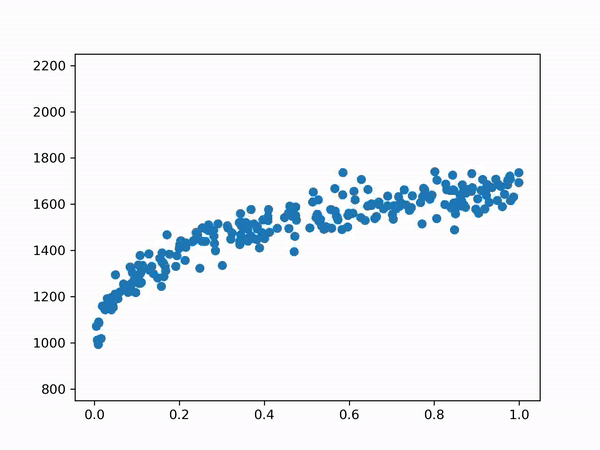
Determining the Likelihood of Winning

If we consider a match between player A and player B, the ELO rating system gives the following winning chance (between 0 and 1):

Obviously, it follows that the probability for player B is equal to 1 minus the value for player A.

Here’s how we’ll write it:

public static class RankingELO {
  // returns probability of winning for player 1
  public static float GetProbabilityWinning(float ratingPlayer1, float ratingPlayer2) {
    return 1f / (1f + Mathf.Pow(10f, (ratingPlayer2 - ratingPlayer1) / 400f));
  }
}

Adjusting the Players’ Ratings

Now that we have both of the player’s winning probability, we can use it to compute the number of points to be added/substracted to the ratings. Since this probability is already dependent on difference in the 2 players’ skills, we include a constant for ratings changes.

public static class RankingELO {
  ...

  public static Vector2 UpdatePlayerRankings(float ratingPlayer1, float ratingPlayer2, float multiplier, bool isPlayer1Winner) {

    float probabilityWinPlayer1 = GetProbabilityWinning(ratingPlayer1, ratingPlayer2);

    if (isPlayer1Winner) {
      ratingPlayer1 += multiplier * (1 - probabilityWinPlayer1);
      // 0 - probabilityWinPlayer2 =  probabilityWinPlayer1 - 1
      ratingPlayer2 += multiplier * (probabilityWinPlayer1 - 1);
    } else {
      ratingPlayer1 += multiplier * (- probabilityWinPlayer1);
      // 1 - probabilityWinPlayer2 = 1 - (1 - probabilityWinPlayer1) = probabilityWinPlayer1
      ratingPlayer2 += multiplier * probabilityWinPlayer1
    }

    return new Vector2(ratingPlayer1, ratingPlayer2);
  }
}

In the code above we called this constant “multiplier”. You are free to set this value, but it is common to change it depending on the number of games played by the player to achieve a desired property in your ranking system (high multiplier fast convergence when the player is new and we must determine its initial ranking, or low multiplier to ensure stability for more experienced players). You can also modify the function to use a different multiplier for both players.

For example, the FIDE (Fédération Internationale des Échecs) uses the following rules for chess (from Wikipedia):

• K = 40, for a player new to the rating list until the completion of events with a total of 30 games and for all players until their 18th birthday, as long as their rating remains under 2300.
• K = 20, for players with a rating always under 2400.
• K = 10, for players with any published rating of at least 2400 and at least 30 games played in previous events. Thereafter it remains permanently at 10.

With this, you should have all you need to implement your own ranking system based on ELO. Have fun with it!